Posted on

Surprise! Reflections on MathsConf23

Based on the MathsConf23 session list, there were 32,400 different sets of workshop selections that delegates could have made. On top of this, each delegate is unique, carrying their own experiences and professional development aims. This means that it is quite possible for different people to attend the same conference and to come out of it with very different key messages to take home. For me, the theme of surprise cropped up a number of times through the day, and I’ve been thinking a lot about it since.

Magical surprises

First up, I attended Magical Maths: Provoking curiosity, run by Ben Sparks and Rob Eastaway. These are two of my favourite people in the Maths world. Seeing Ben’s use of dynamic geometry at various events and on YouTube is one of the reasons I became a GeoGebra enthusiast. Rob’s book, Why do buses come in threes, had a huge influence on me as a child, as I have tweeted a few times, most recently in this thread.

It was therefore a pleasant surprise to hear Rob mention in passing that there is a new edition coming out imminently. The main surprises, however came while watching the tricks Ben and Rob performed during their workshop. Now, I knew about one of the tricks beforehand, and immediately worked out how a later trick involving dice was done–but it was still great to see these accomplished performers’ stagecraft shining through on Zoom via webcam. Of course, there were also things I hadn’t seen and was genuinely blown away by, notably a card trick at the end, and a somewhat more “typical”, Maths puzzle during the session that turned out to be quite delightful to think about. I won’t spoil it by elaborating on it, but if you’re intrigued, you should watch the recording, which I strongly recommend you do.

During the session, I tweeted one of my take-aways, unaware that “surprise” would become my word of the day.

Principles that surprise

The second session of the day was the one in which I delivered my workshop, which I had titled Principles and procedures in geometry. You can download the PowerPoint from here–but before you do, it is worth noting the following:

  • The file size is quite large (approximately 60 MB) because it contains a number of embedded GeoGebra applets.
  • The embedded GeoGebra applets will only function in the PowerPoint if you enable or “trust” the GeoGebra add-in.
  • Many of the slides contain minimal supporting information, as I created them (a) with the intention of speaking over them and (b) with the knowledge that anyone interested in finding out more would have access to the recording of the workshop.

Given all this, I recommend you watch the recording. If you need convincing, check out what people said:

Click here for lots more tweets!

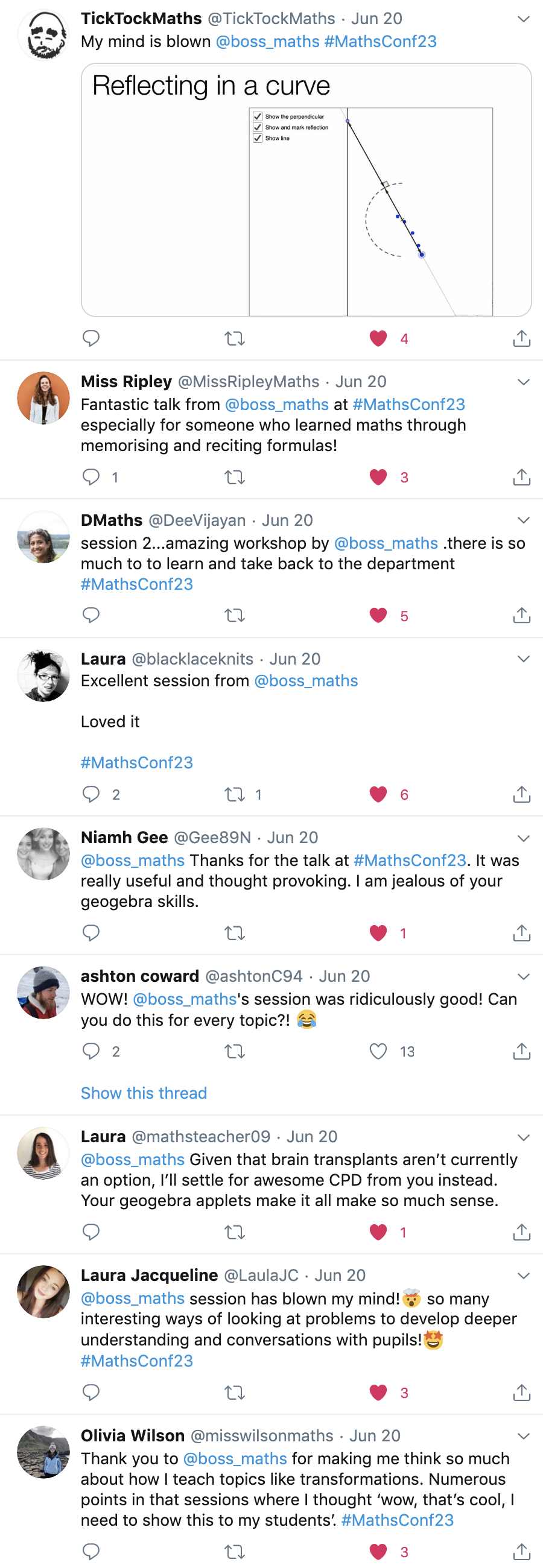
I opened my workshop with a poll designed to surprise. The question was: “Enlarging an object by scale factor greater than 1 always makes the object larger–true or false?”

I think about 95% percent of the respondents voted that this was true, though the Zoom chatbox indicated that many were concerned that this was a trick question–which indeed it was. While a 2D shape does get larger under such an enlargement, a point, for example, does not.

I spent about half of my workshop looking at transformations. Amongst the key principles I want students to appreciate is that transforming an object really involves transforming every point on that object. Sometimes students don’t appreciate this because they are procedurally just transforming a polygon’s vertices and then joining them up–but this is a shortcut that only works because transformations at GCSE always map straight lines to straight lines. To illuminate this, I used an example in which a straight line is reflected in a semi-circular mirror. To obtain the reflection here, students can’t just reflect two points and join them up; they need to reflect several points on the line before they get an idea of what the reflection will look like. This seemed to generate some buzz in the chatbox during the session and on Twitter later! While I was unable to keep up with the chat, I think–at least hope–it did generate some surprise and delight.

I also talked about other topics, including perimeter, area, and volume, but won’t go in to more detail here. In summary, I was suggesting that some (not necessarily all) topics, especially in geometry, lend themselves well to the following approach:

  • Start with a key principle or definition.
  • Devise exercises that force students to spend time working with the principle or definition at hand. These may not look like typical textbook or exam questions.
  • Then introduce formulas and procedures.

After my session, I attended Peter Mattock’s session on Conceptualising Maths. I’d learned a lot from Pete’s workshops in the past and from his excellent book, and his MathsConf23 workshop did not disappoint. Some noticed that both Pete and I were suggesting similar ideas–at least when it came to teaching transformations–but nonetheless I came away with plenty of food for thought.

A good point about surprise

In the afternoon, I attended Kris Boulton’s Always teach “what” before “why” workshop. I think it’s fair to say that Kris’s session generated a lot of buzz! You can read Mr Alhassan’s thoughts here and Jess Prior’s thoughts here. Additionally, Craig Barton shares his perspective of the workshop in his conference takeaway podcast.

I’ll say that it is very much worth watching the recording. Kris is incredibly well-read and thoughtful about what he presents. From my point of view, there was very little controversial in the workshop. I’m still not sure about the titular assertion that we should always teach “what” before “why”, but in the case of indices, I see merit in the argument. Kris argued against starting with an attempted justification of \(a^{m} \times a^{n} = a^{m+n}\). Typically, we might do this with an example like \(5^{3} \times 5^{4} = 5 \times 5 \times 5 \times 5 \times 5 \times 5 \times 5 = 5^{7}\). I’ve always found this a little unsatisfactory because this intuitive demonstration only works with positive integer indices.

So for this particular index law, I’ve often considered treating \(a^{m} \times a^{n} = a^{m+n}\) as axiomatic, and showing that \(5^{3} \times 5^{4} = 5^{7}\) is not a justification but a consequence of the index law–which, pleasingly, perfectly fits in with their intuitive understanding.

This leads me to a particular one of Kris’ arguments that I found quite powerful. The delightful surprise we might experience at a mathematical proof relies on the fact that we know already know the thing being proved. For example, there are a multitude of proofs of Pythagoras’ theorem. As maths teachers, we know the theorem already, and are therefore in a position to be delighted by a proof we’ve not have seen before. To a child that has never encountered Pythagoras’ theorem, showing them a proof at the outset wouldn’t give them same the experience of delight.

A digression on indices

I’m not suggesting the below an abstract approach is an appropriate way to introduce students to index laws, but it is neat to see how much we can deduce about indices starting with just two axioms or rules..

  • Rule 1: \(x^{1} \equiv x\)
  • Rule 2: \(x^{a+b} = x^{a} \times x^{b}\)

(a) Show that \(x^{2} \equiv x \times x\).

   \(x^{2} \equiv x^{1+1} \text{ (since 2 = 1 + 1)}\)

      \(\equiv x^{1} \times x^{1} \text{ (using rule 2)}\)

      \(\equiv x \times x \text{ (using rule 1)}\)

(b) Show that \(x^{3} \equiv x \times x \times x\).

   \(x^{3} \equiv x^{2+1} \text{ (since 3 = 2 + 1)}\)

      \(\equiv x^{2} \times x^{1} \text{ (using rule 2)}\)

      \(\equiv x \times x \times x^{1} \text{ (from (a))}\)

      \(\equiv x \times x \times x \text{ (using rule 1)}\)

(c) Show that \(x^{0} \equiv 1 \text{ for } x \neq 0\).

   \(\text{Note that } x^{1} \equiv x^{1+0} \text{ (since 1 + 0 = 1)}\)

       \(\equiv x^{1} \times x^{0} \text{ (using rule 1)}\)

    \(\text{So }x^{1} \equiv x^{1} \times x^{0}\)

    \(\text{Dividing both sides by } x^{1}, \text{ we see:}\)

      \(1 = x^{0}\)

(d) Show that \(x^{-1} \equiv \dfrac{1}{x}\).

   \(x^{-1} \times x^{1} \equiv x^{0} \text{ (using Rule 2)}\)

   \(x^{-1} \times x \equiv 1 \text{ (using Rule 1 and part (c)}\)

    \(\text{Dividing both sides by } x, \text{ we see:}\)

      \(x^{-1} \equiv \frac{1}{x}\)

A different kind of surprise

As this blog post has now got very long, I won’t go into much more detail here. I attended Dan Draper’s Sequencing an interim curriculum workshop, which was full of really well thought out ideas, before ending the day with Craig Barton’s Misconceptions in Mathematics: Angles workshop. Here again the theme of surprise came up–but in a different way. Where earlier the emphasis was on the kind of surprises we might want our students to experience, this workshop was seemed to be about surprising teachers.

Craig’s workshop was based on a treasure trove of data: thousands of responses to diagnostic questions on his Eedi platform. Looking at thousands of responses–and students’ accompanying explanations–makes it easy to identify the most common misconceptions. In his workshop, Craig used interactive polls to great effect by asking teachers to state what they considered to be the most common wrong answer to a number of diagnostic questions. The results, in some of the cases, were surprising.

As Craig explained, teachers can access the treasure trove of data to get a good sense of what misconceptions are common for each topic. Once you know this, you can begin to pre-empt a lot of these by improving task design.

More surprises yet?

I didn’t catch Dan Pearcy’s workshop live, but I did spot this tweet during the day at a point when I’d already noticed that the recurring theme of surprise:

I look forward to catching up with Dan’s workshop–and, honestly, all the other workshops I couldn’t see live. I made an effort at this conference to choose workshops run by people I’d not seen before (four out of the five workshops I attended were run by people I’d not seen before). I know from attending several of Jo Morgan’s previous workshops that an incredible amount of preparation goes into them–you’ll know how much thought she puts into things if you’ve seen any of her Topic in depth videos or blog posts. I’ve heard a ridiculous amount of good things about Tom Manners’ workshop. Having watched his ResourceFULL series so far, I’m not remotely surprised. I consider myself an etymology enthusiast (see my vocab resource here, which remains my most liked resource on Twitter), so I’m especially looking forward to catching Ed Southall’s workshop too.